Simulating a toy language to explore semantic vectors and biased learning

Semantic vectors, or word embeddings, are a neural network-based representation of the meaning of word, as defined by, e.g., word2vec. The "meaning vector" of a given word is the hidden layer of a network that has been trained to predict the occurrence of surrounding words. The idea is that words that are interchangeable in usage will be found in similar contexts and therefore have similar patterns in the vector that was trained for predictions.

A fascinating question that arises with semantic vectors is: What happens if you apply vector algebra to them? If you take, in terms of their vectors, "King" minus "Male" plus "Female", do you get a vector similar to "Queen". If you play around with a word2vec implementation like Gensim, this does indeed seem to work pretty well.

To get a sense for how word2vec works and how the network gets trained, I used a simulated toy language, with code available on GitHub. In this language, words are simply numbers - "0", "1", "57", "162", etc. The words "0" through "9" are reserved for pairs of words of interest. Each pair, {"0", "1"}, {"2", "3"}, etc, is associated with a common context - that is, each of the pair has a set of surrounding words that consistently occur around them. "0" and "1" are both surrounded by "20", "21", etc; "2" and "3" are both surrounded by "30", "31", etc; and so on.

The core of the language is mapped in this table (the role of bias is introduced below).

Pair	Word	Context	Echoes added as bias	Shared pairs
0	0	20, 21, 22, 23, 24, 25	No	No
0	1	20, 21, 22, 23, 24, 25	No	No
1	2	30, 31, 32, 33, 34, 35	No	No
1	3	30, 31, 32, 33, 34, 35	No	No
2	4	40, 41, 42, 43, 44, 45	Yes	Yes
2	5	40, 41, 42, 43, 44, 45	Yes	No
3	4	50, 51, 52, 53, 54, 55	No	Yes
3	7	50, 51, 52, 53, 54, 55	No	No

In this language, sentences (which will be used as documents in terms of GenSim, where the training corpus is provided by a sequence of documents) are built up of a series of concatenated chunks containing one of a word pair and its context, e.g., ['33', '30', '35', '34', '32', '2', '31']. Chunks are separated by buffer sequences of random words.

So, if everything's working, words within a pair should be more similar than words from different pairs. The pair {"0", "1"} and the pair {"2", "3"} are used to test this basic relationship. Indeed, running simulations shows that the curves over training time show that the distance between "0" and "1" is low and the distance between "0" and "2" is high. (Additionally, unexpectedly, there's also a bit of a funny pattern over time, with an initial peak in dissimilarity that then converges to a lower level.)

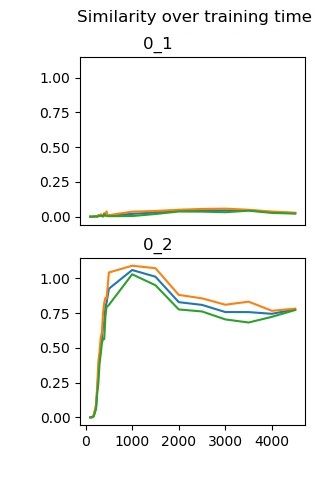
Note that "0" and "1" don't co-occur! They're linked just by their context. It's a different kind of association than a traditional Pavlovian kind of learning.

In models of real language use, biases occur that mirror prejudices (Caliskan et al., 2017), but also reflect, e.g., biophilic tendencies (Gladwin, Markwell & Panno, 2022) and behavioural alcohol-related associations that could help explain addiction (Gladwin, 2022). Much attention has, rightly, been placed on the dangers of using biased models irresponsibly. However, these models could also provide a useful window into human communication and therefore human social and psychological processes.

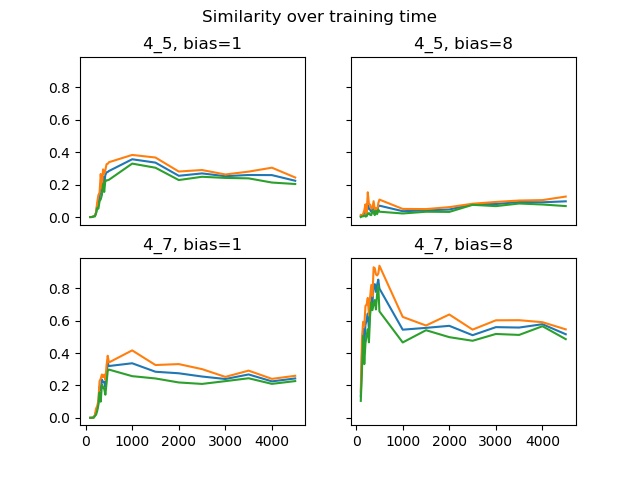
One theoretical possibility is that biases in a trained model reflect abnormal training effects. This was suggested in the context of alcohol-related associations (Gladwin, 2022), since effects of alcohol may include abnormal reinforcement processes. The toy language was used to play with this possibility: for one pair, the {"4", "5"} pair, any occurrence of a sentence containing them and their context was repeated for a number of "echoes". This pair overlapped with a {"4", "7"} pair, which did not have echoes. The hypothesis is, that adding echoes serves to create a bias: "4" becomes more similar to "5" than to "7".

This does indeed result from simulations. When there are no additional echoes (coded here as bias = 1), the "4"-"5" and "4"-"7" similarities are equally mediocre (left hand column). Setting the bias to 8 (right hand column), associating the "4"-"5" pair's context with seven extra echoes, makes "4"-"5" accordingly more similar and "4"-"7" more dissimilar. Whether this "echoing" has anything to do with how the brain might undergo biased learning is, of course, a quite different question. However, obsessive or repeated intrusive thoughts do occur and modeling work like this could produce worthwhile hypotheses on their effects.

Finally, a general conceptual point. It's often questioned how close to human cognition models like this are. I'd suggest treating this as an empirical question, with the traditional truism in mind that all models are false, but some are useful. From the literature, some cited above but also, e.g. Lynott et al., 2012 and Wingfield et al., there are non-trivial, quantitative links between computational models and behavioural or neural patterns. The well-defined processes in the models could be "grafted" theoretically onto broader verbal theories of cognition. Why couldn't the same kind of learning be applied to representations of other entities, processes, and states than just words? Again - of course this will be wrong, like all models. But it's a step and allows more detailed future tests and questions. This view also makes clear that we should be looking for links to particular components of cognition, rather than expecting a relatively simple, focused model to reflect the full human mind. Creating theoretical cyborgs like this also opens up practical usages, such as model-based suggestions for stimulus selection. Discussed further in, e.g., Gladwin, Markwell & Panno (2022) and Gladwin (2022).

The aim of these simulations was very back-to-basics and, of course, there are more sophisticated models. A lot of my interest comes from thinking about how to make a meaningful, empirically-grounded step from verbal to computationally-enhanced theory, and the current first steps are still closer to the simpler models, or elements of models, I think. But the same point about finding the right cognitive analogue may be useful to keep in mind when thinking about complex models with impressive functionality. We're not looking at an analogue of a full mind, but at some components we share, and it would be good to really define which components those are and are not. That could help both valuing current models properly, and suggesting next steps for them, perhaps along the lines of the historical development of cognitive theory.